
| (Este tutorial
supone el conocimiento previo de conceptos básicos de cinemática
y dinámica)
A partir de esta lección nos centraremos en un importante concepto
involucrado en el movimiento de los cuerpos y en todos los fenómenos
físicos, químicos y biológicos: La energía,
y una magnitud íntimamente ligada a ella: El trabajo mecánico.
Trabajo Mecánico
Para tener una definición precisa de trabajo mecánico y comprender
íntegramente su concepto debemos abordar el concepto de magnitudes
vectoriales, pero esto es algo que haremos en la próxima lección
de este mismo curso. Por ahora aceptemos una definición más
simple que resolverá las situaciones problemáticas más
sencillas. Una vez adquirido el concepto intuitivo de Trabajo Mecánico,
estaremos en condiciones de encarar un estudio más riguroso de esta
importante magnitud de la física.
Comencemos con un caso sencillo: Si aplicamos una fuerza sobre un cuerpo
para desplazarlo a lo largo de una línea recta, éste se moverá
desde su posición inicial hasta una nueva posición. El producto
de la fuerza aplicada por el desplazamiento experimentado por el cuerpo
será, en este caso, el valor del Trabajo Mecánico, es decir:
|
|
Trabajo
= Fuerza x Desplazamiento
|
| Es fácil
ver que para calcular el valor de la fuerza o el desplazamiento para obtener
un trabajo dado podemos despejar:
Fuerza =
Trabajo / Desplazamiento
Desplazamiento
= Trabajo / Fuerza
La unidad de medida del Trabajo Mecánico en el sistema MKS es el
Joule
(se pronuncia yul) en honor del físico inglés James P. Joule
(1818-1889) quien, entre otros importantes trabajos, realizó una
serie de experimentos con los cuales demostró que el calor es una
forma de energía.
1
Joule es igual al producto de 1 Newton (fuerza) por 1 metro
(desplazamiento)
Ejemplo
3-1:
Un hombre empuja una caja de mercaderías en un depósito,
para trasladarla a una posición distante 2m de la posición
en la que se encontraba. Si la fuerza aplicada es de 300N ¿Cuál
es el trabajo mecánico realizado por el hombre sobre la caja?
Solución:
Por simple aplicación de la ecuación anterior podemos verificar
que el Trabajo Mecánico es de 600 Joules, es decir 300N x 2m.
|
1 La unidad
de Fuerza en el Sistema MKS o Internacional es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
2 El Trabajo
Mecánico resulta del producto de:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
3 La unidad
de Trabajo en el Sistema MKS o Internacional es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
4 El Trabajo
Mecánico realizado sobre un cuerpo que se desplaza 5m por acción
de una fuerza de 150N es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
5 La Fuerza
aplicada sobre un cuerpo para trasladarlo 12 metros, realizando un trabajo
de 1320 Joules es de:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
6 Si una fuerza
de 1800N impulsa un automóvil realizando sobre él un
trabajo de 36000 J, éste se desplaza :
(Puede ser
correcta una respuesta, más de una o ninguna)
|
|
Magnitudes Escalares y
Vectoriales
Hasta aquí todo es tan sencillo como multiplicar la fuerza por el
desplazamiento y obtener el trabajo mecánico, aunque, en realidad,
esto es así sólo cuando, como en los ejemplos anteriores,
la fuerza y el desplazamiento están dirigidos según la misma
dirección y sentido y aquí es donde debemos analizar el carácter
vectorial de estas magnitudes.
Tanto la fuerza aplicada a un cuerpo como el desplazamiento que éste
experimenta, sólo quedan completamente definidos si se especifica,
además del módulo, la dirección y el sentido en cada
caso. Por ejemplo, podríamos definir el desplazamiento de un objeto
diciendo, "se movió 3 metros hacia el noroeste" o una fuerza aplicada
sobre dicho cuerpo diciendo "se aplicaron 50 Newton en dirección
norte-sur". Una magnitud así definida se llama magnitud vectorial
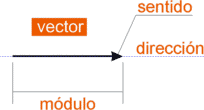
y el elemento que la representa es un vector. Como vemos las
características de un vector son:
|
|
-
Módulo: Indica el menor o mayor valor asignado a la magnitud.
Ejemplo: 3m, 50N, 9,8m/s2
- Dirección:
Especifica la recta de acción del vector. Ejemplo: "dirección
norte-sur", "formando un ángulo de 20º con la horizontal"
ó "según el eje x"
- Sentido:
Para una dirección dada debemos especificar hacia dónde se
dirige el vector, es decir "de norte a sur o de sur a norte" o "hacia
las x positivas o hacia las negativas" |
| Son ejemplos
de magnitudes vectoriales: la velocidad, la aceleración,
la fuerza, el desplazamiento. En cambio son magnitudes escalares:
el tiempo, la posición, la masa, el trabajo, la energía.
Estas últimas no requieren, para quedar definidas, especificar dirección
ni sentido. (no decimos "transcurrieron 15 segundos en tal o cuál
dirección", sólo "transcurrieron 15 segundos")
El Trabajo como producto
escalar
Ahora que tenemos claro que tanto el desplazamiento de un móvil
como la fuerza aplicada sobre él quedan definidos por vectores,
podemos dar una definición más general para el trabajo mecánico: |
| El Trabajo
Mecánico realizado por una fuerza sobre un cuerpo es el producto
entre los módulos de los vectores fuerza y desplazamiento y el coseno
del ángulo que forman dichos vectores entre sí |
Usamos barras
verticales para indicar módulo de un vector, de modo que la expresión
|F| se lee "módulo del vector fuerza" y la expresión |v|=
25 m/seg se lee "el módulo de la velocidad es 25 metros sobre segundo".
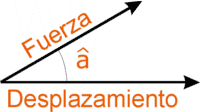
Usando esta notación y la definición de trabajo mecánico
anterior podemos escribir: |
|
T
= |F|.|D|.cos a
;siendo a
el ángulo formado entre los vectores fuerza y desplazamiento |
| Observa que
lo único que se ha modificado respecto del modo de cálculo
anterior es el agregado del factor cos a. Si tratamos
de resolver el ejemplo de la sección anterior con esta nueva ecuación
deberíamos llegar a idéntico resultado. Para verificar esto,
reproducimos el enunciado del problema a continuación...
Ejemplo
3-1:
Un hombre empuja una caja de mercaderías en un depósito,
para trasladarla a una posición distante 2m de la posición
en la que se encontraba. Si la fuerza aplicada es de 300N ¿Cuál
es el trabajo mecánico realizado por el hombre sobre la caja?
... y lo resolvemos:
T = |F|.|D|.cos
a
T = 300N
. 2m . cos 0º
donde colocamos
el ángulo de 0º porque la fuerza y el desplazamiento, en este
caso, tienen igual dirección y sentido. Como el coseno de 0º
es igual a 1, el producto da por resultado 600Nm, es decir:
T = 600
Joules
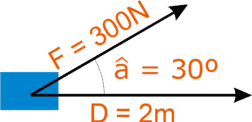
Veamos otro
ejemplo en el que los vectores fuerza y desplazamiento no coinciden en
dirección: |
|
Ejemplo
3-2:
El hombre del ejemplo anterior tira de la misma caja con una soga arrastrándola
por el suelo, pero ejerciendo la fuerza con un ángulo de inclinación
de 30º respecto de la horizontal, como muestra la figura. Si el módulo
de la fuerza es de 300N y la caja se desplaza 2m ¿Cuál es
el valor del trabajo mecánico? |
Solución:
Aplicando la ecuación vista:
T
= |F|.|D|.cos a
T = 300N
. 2m . cos 30º
T = 600Nm
. 0,866
T = 519,6
Joules
La
operación de producto de los módulos de los dos vectores
y el coseno del ángulo que forman entre ellos se llama producto
escalar de dos vectores. Observa que se parte de dos cantidades
vectoriales (fuerza y desplazamiento) y se obtiene un escalar (trabajo
mecánico). Es decir que...
"El trabajo
mecánico realizado por una fuerza sobre un cuerpo es igual al producto
escalar de la fuerza por el desplazamiento experimentado por dicho cuerpo"
Nota:
De acuerdo al ángulo entre los vectores fuerza y desplazamiento
el trabajo puede ser positivo, negativo o nulo, a pesar de que los módulos
de los vectores son siempre cantidades positivas, ya que el coseno del
ángulo puede variar entre -1 y 1 pasando por 0. Toma en cuenta este
hecho al resolver las actividades siguientes
|
7 ¿Cuáles
de las siguientes magnitudes son vectoriales?
(Puede ser
correcta una respuesta, más de una o ninguna)
|
8 ¿Cuáles
de las siguientes son características de un vector?
(Puede ser
correcta una respuesta, más de una o ninguna)
|
9 Un motor
tira de una carga ejerciendo sobre ella una fuerza de 1500N por medio de
una soga. Si la soga está dispuesta verticalmente y la carga asciende
12m según la misma dirección, el trabajo efectuado por el
motor sobre la carga es de:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
10 El Trabajo
Mecánico realizado sobre un cuerpo que se desplaza 5m por acción
de una fuerza de 150N, cuando el ángulo entre el vector fuerza y
el vector desplazamiento es de 60º es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
11 El trabajo
mecánico efectuado por una fuerza de 10N sobre un cuerpo que se
desplaza 8m en forma perpendicular a la fuerza es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
12 Si una
fuerza de 1800N trata de sostener un cuerpo en la cima de un plano inclinado
de 5m de longitud, pero éste resbala recorriendo todo el plano con
igual dirección pero sentido opuesto a la fuerza, el trabajo realizado
por la fuerza sobre el cuerpo es:
(Puede ser
correcta una respuesta, más de una o ninguna)
|
|